【 数学・物理学 編 】 完全数について Wikiiに、【 完全数とは、自分自身を除く 正の約数の和に等しくなる自然数のことである 完全数の最初の3個は 6 (= 1 + 2 + 3)、28 (= 1 + 2 + 4 + 7 + 14) 496 (= 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248) である 「完全数」は「万物は数なり」と考えた ピタゴラスが名付けた数の一つであることに由来するが なぜ「完全」と考えたのかについては何も書き残されていないようである 中世の『聖書』の研究者は 6 は「神が世界を創造した(天地創造)6日間」 28 は「月の公転周期」で、これら2つの数は地上と天界における 神の完全性を象徴していると考えたとされる 古代ギリシアの数学者は 他にもあと2つの完全数 (496, 8128) を知っていた 以来、完全数はどれだけあるのかの探求が 2500年以上のちの現在まで続けられている 】 とありましたが、完全数で、面白い話はありますか? と、教授にお尋ねしてみました 教授: うーん、完全数ってそもそもよく分かっていないんですよね 現在、50個だか51個しか発見されてなかったと思います にもかかわらず、完全数は無限にあるのではないかと言われてたりします 見つかっている最大の完全数は、約5000万桁だと思うんだけど (^^;;; ちなみに、素数(1 と自分自身以外に正の約数を持たない自然数で 1 でない数)は 2 以外はすべて奇数ですが 完全数は、今のところ偶数しか見つかってないんですよ 但し、奇数の完全数が存在しないと証明されたわけではないので あったとしても不思議ではないのですが・・・・ 偶数の完全数を見つけるにはメルセンヌ素数を見つければいいので 実際には計算機でメルセンヌ素数を見つけています 【 メルセンヌ素数とは、2^n-1 = の素数 nが2の場合の3 nが3の場合の7 など 】 ちなみに、通常の素数判定は1000桁でもひどく時間がかかる難しさで 5000万桁の整数の素数判定なんて太陽系が滅んでも無理なので 笑 メルセンヌ素数に特化した素数判定アルゴリズムを用いて調べています # 完全数であることを調べるために 全ての約数を求めて、足し算して確かめているわけではない あと、正の整数 n が完全数であるための必要十分条件が n の全ての約数について、逆数の和を計算すると 2 になることされています # 簡単に証明できます 例えば、完全数である 6 の約数は 1, 2, 3, 6 ですが この4つの逆数をすべて足すと (1/1) + (1/2) + (1/3) + (1/6) = 2 28であれば、約数は 1, 2, 4, 7, 14, 28 で (1/1) + (1/2) + (1/4) + (1/7) + (1/14) + (1/28) = 2 逆に、これを満たす数は完全数であることも言えます (要するに、完全数でないならば 2 にはならないと言えます) この性質から完全数は調和数になるとされています 【 調和数は、約数の調和平均(逆数の平均の逆数)が整数になる数 完全数ほどでないが、かなり珍しいらしい 例えば、6 の約数は 1、2、3、6 なので これらの逆数の平均は、(1+1/2+1/3+1/6)÷4=1/2 そのまた逆数なので調和平均は 2 2は整数でなので 6 は調和数 】 緋山: 最大の完全数は約5000万桁というのも驚きですが 5000万桁の整数の素数判定は太陽系が滅んでも無理 というのが驚愕です!! 太陽系が滅んでも無理 って コンピュータでも無理ということですか? 教授: はい、今あるスパコンより速いコンピュータを使っても無理です 素数の判定を行うときに最も素朴な方法は 2で割り切れるか? 3で割り切れるか?・・・・ と小さい数で割っていって どの数でも割り切れなければ素数というやつです これ、例えば、532343 が素数であるかどうかを確かめるためには √532343 = 729.6... 以下の最大の整数 = 729 まで 確かめればよいことになります 要するに729回割り算を行えば素数であるかどうかが判定できます 【 平方根は2乗する前の数で 1の平方根は、1と-1 4の平方根は、2と-2 】 ここで、整数の平方根を取ると 桁数が大体半分になるということに注意してください 上の例だと6桁の整数が3桁になっています 同じ方法で5000万桁ある整数が素数であるかを判定すると (2500万桁の整数)回の割り算を行うことになります まあ、これは悪すぎるので 現在知られている最速の素数判定法を用いるとして それでも(100桁の整数)回の割り算が必要になります 桁数が格段に小さくなったことを確認しておいてください # 2500万桁 → 100桁 ですから さて、この100桁の計算が何年かかるかを計算してみたいと思います まず、1年は何秒かご存知です? 1年 = 365 × 24 × 60 × 60 = 31,536,000秒 ざっくり言えば 3千万秒しかないんです 数値そのものよりも桁数を数えてください。8桁です 1秒間に何回割り算を実行できるかわからないですが 5000万桁もある整数を使った割り算なので それだけで時間がかかります 仮に1秒間に1億回の割り算を実行できたとしましょう (実際にはスパコンでも無理だと思いますが) すると、1年間で1億 × 3千万 = 約3千兆回の割り算を 実行できることになります。3千兆は16桁です 100桁の整数を、3000兆回で割れば何年かかるか分かりますが この年数の桁は、整数の桁-割り算回数の桁 と、だいたい一致します 例えば、34兆(14桁の整数)を 割り算の回数 2万(5桁)で割ると、年数は17億(10桁) 14 - 5 = 9桁(年数)とは、せいぜい 1桁違うくらいです なので 100桁の整数 ÷ 3000兆 (16桁) = 100 - 16 = 84 (およそ85) 100桁の整数の素数判定するのには 85桁くらいの年数を必要とします 太陽を含めた恒星の寿命は 100億年と言われていて 100億はたったの 11桁です ということで、太陽が消滅=太陽系が滅亡しても まだ計算は始まったばかりという段階です (^^;;; ちなみに、1000桁程度の整数でさえ 割り算の回数が40桁の整数になるので 年数は40 - 16 = 24桁の整数になって 太陽系の寿命よりはるかに長いのです 【 5000万桁の整数の素数判定 → (100桁の整数)回の割り算 → 100桁の整数 ÷ 3000兆(16桁) = 100 - 16 = (84桁の整数)年かかる 1000桁の整数の素数判定 → (40桁の整数)回の割り算 → 40桁の整数 ÷ 3000兆(16桁) = 40 - 16 = (24桁の整数)年かかる 】 緋山: ≪見つかっている最大の完全数は、5000万桁≫ というのは、メルセンヌ素数に特化した 素数判定アルゴリズムを用いて調べたわけですね 教授: そうです。そうでないと調べられません リュカ-レーマー・テストというのがあるそうですよ これだと、掛け算+割り算のセットを1秒間に1回しか 実行できなかったとしても3年かからずに判定できます 実際にはもっと高速にできるかもしれないし、できないかもしれませんが 遅かったとしてもせいぜい10年単位の仕事ということになると思います リュカ-レーマー・テスト は 入力がメルセンヌ数に制限されているため 全ての自然数に対して素数判定を行うわけではありません 入力が制限されているために 5000万桁あっても素数判定が3年かからずできるわけです 緋山: ついでといってはなんですが 「メルセンヌ素数に特化した素数判定アルゴリズム」 というのもごく簡単に説明してもらえますか? 【 アルゴリズムとは、コンピューター(計算機)で、問題を解く手法のこと その「やり方」を工夫して、より良いやり方を見つけよう というのが、アルゴリズムの研究 だとされます 例えば、乗換検索のアプリなんかで出発駅と目的駅を入れたら 経路がいくつか出てきますが こういうものを求めるときに どうやったら短い時間で求められるか? を考えるのがアルゴリズム屋さん だそうです 】 教授: 正の整数 n に対して Mn = 2^n -1 を n 番目の「メルセンヌ数」と言います M1 = 2^1 - 1 = 2 - 1 = 1 M2 = 2^2 - 1 = 4 - 1 = 3 M3 = 2^3 - 1 = 8 - 1 = 7 M4 = 2^4 -1 = 16 - 1 = 15 (= 3 × 5) M5 = 2^5 - 1 = 32 - 1 = 31 M6 = 2^6 - 1 = 64 - 1 = 63 (= 3 × 3 × 7) (以下無限に続く) で、Mn の中で素数であるものを「メルセンヌ素数」(Mp)と言います 上の例でいえば、M2, M3, M5 がメルセンヌ素数です 実は「Mn が素数であるならば n は素数である」ことが証明されています 逆に言えば、n が素数でなければ Mn も素数にはなりません 例えば、1, 4, 6 は素数ではないので、M1, M4, M6 は素数にはなりません 適当に、n = 10 としても M10 は素数にはならないはずです (実際、M10 = 1024 - 1 = 1023 = 3 × 11 × 31 なので、素数ではないです) ここで、メルセンヌ素数のときに Mp と書いて メルセンヌ数のときには Mn と書いていますが n は natural number(自然数)を取る変数を p は prime number(素数) を取る変数を表しています # メルセンヌ素数の場合には n が 素数に限定されるので n の代わりに p を用いることが多いです 注意してほしいのは n が素数だからと言って、Mn が素数になるとは限りません 仮に「n が素数であるならば Mn も素数である」 が成り立っているならば n が素数であることを確認すればいい訳ですが n が素数だからと言って、Mn が素数になるとは限らないので メルセンヌ数が素数であることを確認するためには 何かいいアルゴリズムが必要になります それが先ほどのリュカ-レーマー・テストです リュカ-レーマー・テストでは p が奇素数であるメルセンヌ数 Mp が与えられて (正確には奇素数 p が与えられて) Mp が 素数であるかどうかを判定するアルゴリズムです ですので、実際には p から Mp を計算して(これは実は難しくない) それからMp が素数であるかどうかを判定します ≪実は「Mn が素数であるならば n は素数である」ことが証明されています 逆に言えば、n が素数でなければ Mn も素数にはなりません≫ これについて、証明がさほど難しくないので説明しておきましょう 知らなくても構わない話なので、難しかったら読み飛ばしてください 笑 まず、Mn ですが、これを2進数で表すと 1 が n 個ならんだ数になります 例えば1 が 5 個並んだ数 ( = M5) を 10進数の 11,111 と区別するために 、2進数では [11111]_2 と書きます 要するに、M8 = [11111111]_2 (2進数) = 255 (10進数)ということです もし n が素数でないとすると、n = r × q と書くことができます (nは、自分と1以外に、r と q で割れ切れることになる) r と q は2以上の整数です n = r × q のとき n 個の 1 の列は、先頭から r 個ずつに 分けると 長さが r の 1 の列が q 個できます 例えば、上の M8 の場合、 2 × 4 = 8 なので 先頭から 2 (r) 個ずつに分けてあげると ちょうど 4 (q) 個に分けることができます 同様に、Mn = [111....1]_2 は Mp = [11...1]_2 で割り切ることができます (なお、nとpは、何番目を表わす記号で p自体が素数という意味ではないので注意) どうしてかというと 2進数上で、最下位の桁を 1 として あとは上位に行くにしたがって p-1 個おきに 1 を、それ以外は 0 として 1 が q 個になるまで並べてあげた 2進数と Mp をかけると Mn になるからです Mn = Mp × 【 最下位の桁を 1 として 、p-1 個おきに 1 を それ以外は 0 として、1 が q 個になるまで並べてあげた 2進数】 です ちょっとわかりにくいかもしれませんが 先ほどの M8 の場合だと Mn→ M8 (8番目のメルセンヌ数) = 255 (10進数) = [11111111]_2 (2進数) Mp→ M2 (2番目のメルセンヌ素数) = 3 (10進数) = [11]_2 (2進数) です 255 = [11111111]_2 = [11]_2 × [1010101]_2 = 3× 85 となります これが n = 9 だとしたら Mn→ M9 (9番目のメルセンヌ数) = 511 (10進数) = [111111111]_2 (2進数) Mp→ M3 (3番目のメルセンヌ素数) = 7(10進数) = [111]_2 (2進数) です 511 = [111111111]_2 = [111]_2 × [1001001]_2 = 7 × 73 となります M8 の場合だと、3と85で割り切れるので 8(n)は、素数でない → M8(Mn) =255は、素数でない が成立 M9 の場合だと、7と73で割り切れるので 9(n)は、素数でない → M9(Mn) = 511は、 素数でない が成立 ですので、n が素数でないならば Mn も素数でないことが 証明できたことになります 例えば、M1000なんて大きすぎて計算したくないですが 笑 こんな大きな数でも 1000が素数ではないので どんな数かは分からなくても M1000が素数でないことが分かります 2進数を説明しておくと、 2進数の [a b c d e f]_2 を10進数に直すと a × 2^5 + b × 2^4 + c × 2^3 + d × 2^2 + e × 2^1 + f × 2^0 = 32a + 16b + 8c + 4d + 2e + f になります 7桁の2進数ならば、最上位の数×2^6 から始まります 【 2^0が1 なのは、正確には 2^3 とは 1×2×2×2 2^2 とは 1×2×2 2^1 とは 1×2 2^0とは 1 であり 一つ下の値は、上の値を2で割った数になるので 2^0の値は、一つ上の2を2で割った数になるから 】 M8 = 255 = [11111111]_2 = [11]_2 × [1010101]_2 = 3× 85 でいうと [11]_2 は 2桁の2進数なので、最上位の数×2^1 から始まり 1×2^1 + 1 = 3 になります [1010101]_2 は 7桁の2進数なので、最上位の数×2^6 から始まり 1× 2^6 + 0 + 1× 2^4 + 0 + 1× 2^2 + 0 + 1× 2^0 = 64 + 16 + 4 + 1 = 85 になります M9 = 511 = [111111111]_2 = [111]_2 × [1001001]_2 = 7 × 73 でいうと [111]_2 は 3桁の2進数なので、最上位の数×2^2から始まり 1×2^2 + 1×2^1 + 1 = 7 になります [1001001]_2 は 7桁の2進数なので、最上位の数×2^6 から始まり 1× 2^6 + 0 + 0 + 1× 2^3 + 0 + 0 + 1 = 73 になります  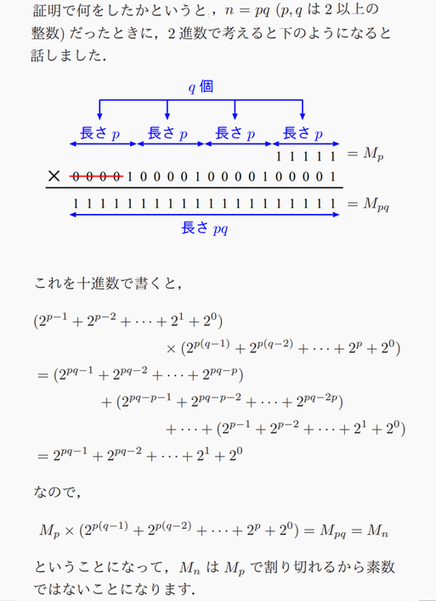 2進数の [a b c d e f]_2 を10進数に直すと (a × 2^5) + (b × 2^4) + (c × 2^3) + (d × 2^2) + (e × 2^1) + (f × 2^0) なので Mp = [11…11]_2 は (1 × 2^p-1) + (1× 2^p-2) + … +(1 × 2^1) + (1 × 2^0) → 2^p-1 + 2^p-2 + … + 2^1 + 2^0 最下位の桁を 1 として あとは上位に行くにしたがって p-1 個おきに 1 を、それ以外は 0 として 1 が q 個になるまで並べてあげた 2進数は 100…0100…100…01 になる 2進数の [a b c d e f]_2 を10進数に直すと (a × 2^5) + (b × 2^4) + (c × 2^3) + (d × 2^2) + (e × 2^1) + (f × 2^0) つまり a b c d e f は、6個 なので、q = 6 (a × 2^q-1) + (b × 2^q-2) + (c × 2^q-3) + (d × 2^q-4) + (e × 2^q-5) + (f × 2^q-q) 100…0100…100…01 (数字は q 個) 十進数になおすと、2^q-1 から始まるので 2^{p(q-1)} + 2^{p(q-2)} + … + 2^p + 2^0 なる 【 1番右の桁の 1が、1 × 2^0 右から p+1桁目の1が、1 × 2^p 右から 2p+1桁目の1が、1 × 2^{2p} … 右から (q-2)p+1桁目の1が、2^{(q-2)p} 右から(q-1)p+1桁目の1が2^{(q-1)p} 】 # 2進数で下x桁が1のときに、十進数で 2^{x-1} が足されています 緋山: 2の0乗が1になる これについても、ちゃんと知りたくなり サイトをあちこち調べると 2の0乗は、2のn乗÷2のn乗を約分すると 分母と分子はおなじだから1になる とありましたが、釈然としません (T_T) 指数(a^nのn)を使った計算では ・掛け算は指数の肩が足し算 ・割り算は指数の肩が引き算 になります 例えば、2^3 × 2^5 = 2^{3+5} = 2^8 となります 2^3 = 2 を 3 回かけた数 2^5 = 2 を 5 回かけた数 なので、二つの数を掛けたら 2 を 3 + 5 = 8 回かけた数になるのは大丈夫ですよね? 同じように、2^5 ÷ 2^3 = 2^{5-3} = 2^2 となるのだけど 割り算は分数なので、2^5 / 2^3 と書いてみて約分します 要するに、(2 × 2 × 2 × 2 × 2)/(2 × 2 × 2) を約分すると 分子と分母から 2 が 3 個ずつ消えるので 分子は 2 × 2、分母は 1 になって 2 × 2 になります これが 2^5 ÷ 2^3 = 2^{5-3} の意味です では、2^4 ÷ 2^4 ですが もちろん答えは 1 なのですが これも指数のルールを 同じように適用できると都合がいいので 2^4 ÷ 2^4 = 2^{4-4} = 2^0 を 1 としたのです こうしとくことで指数の肩が 0以上の整数でも適用できて便利だからです 同じ理由で、指数の肩が負の数のときも 2^{-2} = 1/(2^2) というように定義しました これは、2^3 ÷ 2^5 を考えると わかりやすいと思いますが (2 × 2 × 2) / (2 × 2 × 2 × 2 × 2) = 1/ (2 × 2) = 1/(2^2) となる一方 指数の計算のルールの通りに書いてみると 2^3 ÷2^5 = 2^{3-5} = 2^{-2} となるので 2^{-2} = 1/(2^2) と定義したのです こうすることで 指数の肩が整数なら何でもよくなって計算が楽になる ということで 2^0 = 1 だし、2^{-2} = 1/(2^2) なのです # これをさらに拡張することで 指数の肩には実数だけでなく 複素数まで乗るようになりました (^^;;; 数学の空間次元と 超弦理論の次元の式 自然科学の証明と数学の証明 (ひとつ戻る) |
|