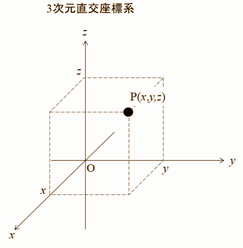
【 数学・物理学 編 】 数学における空間次元とは? 3次元空間の直交座標系は、空間内で 互いに直交する3本の数直線 x軸、 y軸、z軸を 決めることによって定められます
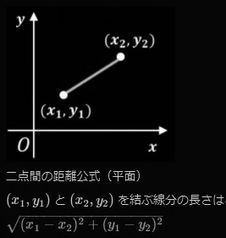
(y軸、z軸は、平面上にあり、x軸は、平面から手前に出ています イメージ的には、紙の上から斜めにペンが手前に出ているような感じ) しかし、4次元の座標というのは存在していません つまり、誰も描くことができません にも関わらず 数学では、4次元、5次元・・・・ n次元 も表わせるといいます これについても簡単に説明してもらえますか? と、知り合いのアルゴリズムの教授に聞いてみました 我々のいる世界では (実際に何次元で構成されているかはともかく) 人間は、3次元までしか認識できないわけですが ベクトルの成分の個数を増やしてあげれば 何次元でも表現できて、【数学の上】では n次元空間を表現することができます 「n次元なんて実際にあるのか?」という質問は 数学では愚問で、モデルとして成立する(矛盾しない) ならば存在すると考えるのが数学です 数学はあくまで数学の中という 閉じた世界で、理論を組み立てているので 物理とか、他のところで使えるかはどうでもいい話なのです 4次元なら4つの整数、 5次元なら5つの整数を使う ということですか? そうです 4次元空間のベクトルや点の座標を (3, -2, 5, 1) みたいに表します かっこの中に並べる実数の数が増えれば次元が増える という話です それだけの話なのですが 2次元で定義されているいろんな概念が 4次元でも5次元でも同じように定義されるのですよ 2次元で定義されている概念が4次元でも5次元でも 同じように定義される というのは? なんでもと言っていいかもしれません 例えば、2次元平面上の2点(3, 4), (5, 2)間の距離は √{(3-5)^2 + (4-2)^2} = √{(-2)^2 + 2^2 } = √(4 + 4) = √8 = 2√2 と求めます
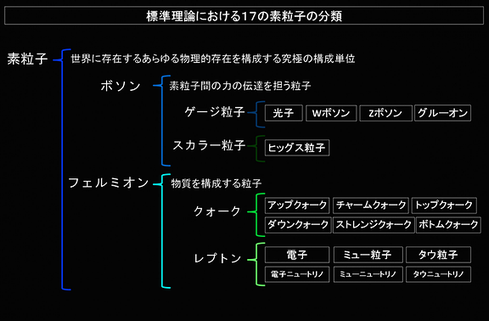
この2点を通る直線の方程式は a=(3,4), b=(5,2) , x =(x, y) とおくと x = t a + (1-t) b (ただし、t は任意の実数) というように表すことができます 同じように 4次元空間上の2点(3, 1, 5, 2), (4, 4, 1, 5) 間の距離は √{(3-4)^2 + (1-4)^2 + (5-1)^2 + (2-5)^2} = √{(-1)^2 + (-3)^2 + 4^2 + (-3)^2}= √(1 + 9 + 16 + 9) = √35 というように求めます この2点間を通る直線の方程式は a=(3, 1, 5, 2), b=(4, 4, 1, 5) , x =(x, y, z, w) とおくと x = t a + (1-t) b (ただし、t は任意の実数) というように表すことができます 何も変わらないのです ベクトルの内積(ベクトル同士の特殊な掛け算)も同じです 2次元平面上の2つのベクトル(5, 1), (2, 3) の内積は 【 (5, 1), (2, 3)とは、➝ の先っぽの点の座標での位置です 】 5×2 + 1×3 = 10 + 3 = 13 と求めますが 4次元空間上の2つのベクトル (3, 1, 3, 4), (1, 2, 5, 3) の内積も 3×1 + 1×2 + 3×5 + 4×3 = 3 + 2 + 15 + 12 = 32 と求めます 超弦理論の次元の式 超弦理論とは 物質の最小単位は粒子ではなく 原子や素粒子よりもはるかに小さいヒモであるとします それまで、物質を構成する基本は0次元(点)の粒子である と考えられていましたが そうではなく1次元の「ヒモ」としたところに面白さがあります ひもには、糸くずのような形のものと 輪ゴムのような形のものがあるといいます 現在、知られている素粒子は、数100種類あるらしいのですが 超弦理論では、ヒモがエネルギーを与えられて振動するとき 振動数の違いで、異なる素粒子のように見えているだけである と考えます そして、このようなヒモが10次元の真空にいっぱい詰まっている 10次元のうち6次元は、ヒモの中に閉じこめられていて 残りの4次元、すなわち3次元+時間が、我々の宇宙だ考えます 「銀河も、惑星も、生命も バイオリンのヒモが奏でるメロディーのようなものだ」 といった譬え話がよくなされています 最終的には、5つの超弦理論が誕生し 26次元のひもを考える理論なんかもあったらしく これら5つの超弦理論を統合したのが 11次元〔空間次元が10個、時間次元が1個〕を説く 「M理論」(ブレーン理論・膜理論)です 超ひもの次元を上げて、物質の根源を2次元の膜とした理論だそうです M理論の構成要素は、「メンブレーン」(2次元の膜)と呼ばれる 0から9までの次元をとりうる物体らしいです M理論では、宇宙を、泡状構造体と考え いくつもくっついたシャボン玉(たくさんの宇宙)の1つが 我々の宇宙であると考えるようです 我々の宇宙は 「泡だらけの海に浮かぶ1個の小さな泡」なんて表現されます また、重力が弱いことについて 重力が膜の近くに集中する だから他の場所では重力が弱いと説明します またビッグバンとは、膜が波打っていることから 膜同士の衝突によって発生するもので この衝突エネルギーによって、恒星・惑星・銀河など多くの物質が 生み出されたと説明するようです 但し、こうした理論は、物理学者が ご飯を食べるためのものでしかないので 構成要素が3次元、また5次元の膜であったり 11次元のうち、9次元までが空間次元で あと2つは時間と重力子であるとする立場もあるようです また9つの次元のひもは 3次元の膜に、ひもの両端っこがくっいていて 離れることができないが 重力子だけは閉じていて、別の次元を行き来しているので その分、力が弱くなっているといった考えもあるようです 【 10次元のうち6次元は、ヒモの中に閉じこめられていて 残りの4次元、すなわち3次元+時間が、我々の宇宙 】 とは、なにを根拠としているのでしょうか? 世界が1次元(線)だったと仮定しましょう 存在の位置を示すのに、線上にある物体は 右から10センチというように 1つの数字で位置を示すことができるから1次元です しかし、線がある太さをもっていたとき ありんこの位置を示すのに、縦、横、高さの3つが、必要となる つまり、ありんこにとっては3次元も 我々にとっての1次元となる 同様に、3次元を超える6つの次元は 小さくまるまっていて (コンパクト化) 我々には、認識できない といったようなアホみたいな話を根拠としているのです 9次元というのは、なにを根拠にしているか? これを、述べておきましょう 素粒子の違い = 紐の振動の仕方の違い E = mc^2 重い素粒子ほど、振動が激しい (質量が大きい=エネルギーが大きい) 3次元では、縦方向と奥行きの方向の2つ方向しか 振動方向がない 現在発見されている素粒子は17種類ある
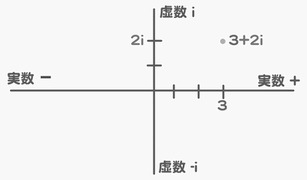
17種類の振動を表現するには、9次元が必要 ということらしい です 「次元」の定義すらできないのに こういうインチキ理論を立てるのは 時間の定義もなしに 「相対性理論は正しい」という馬鹿話と全く一緒ですよ(笑) こういうのはホントは物理ではないですから(笑) 反論があるなら、これに答えろよ!! 【 相対性理論は、時間の刻みが遅れる という話なので、当然、時間の遅れは蓄積されなければならない 地上と東京タワーの展望台とでは 東京タワーの展望台の方が未来にあることになる(笑) 現在と未来は、スマホでやりとりできないでしょ 】 現代物理というのが どこまで、人を馬鹿にして 人を騙して、飯食って、いい思いしているのか という話になるということです 超弦理論を、ウィキペディアで調べると 【 この理論を実証するための実験に必要なエネルギー量は おおよそ人類に扱える範囲を大幅に上回っていると想定されるため そもそも「実証不可能」「永久に仮説」ともいわれる 】とありました 【 多次元を立証すれば、超弦理論の大きな傍証になる しかしそれには、全地球と人が使う エネルギー10年分を一度に使わなければならない 】 とか言っている物理学者さんもいます デタラメはよしてくださいよ(笑) これは、≪多次元≫という言葉に バーチャル的な世界をのっけて 人間を言葉の世界に引きずり込むことです 宗教のすることと本質的になんら変わりません 人間である以上、誰であれ 五次元の世界など、思考も、想像も、表現もできないはずです 「多次元世界」「宇宙の果て」「宇宙の形」 こうした究極的な問題については 物理学者でも、数学者でも、そこらへんの一般人でも 解答に、さほどの違いはないですよ(笑) 「神」とか「霊」の存在を、科学として証明する というのだって話としては矛盾がありません しかし、概念のない存在の いったいなにを証明するのですか? という話なのです 超弦理論の次元(D)を求める式が 2+3×(D-1)×(1+2+3+‥‥)=0 1+2+3+‥‥=-1/12 (18世紀の数学者オイラーの自然数の和の公式) なので 計算すると、D=9 になります この9次元に、時間の次元を加えて10次元としたり さらに、弦と弦に働くの力が強いと生じる次元 なんていうのを加えて11次元とするという立場もあるようです そして、超弦理論というのは、世界は3次元ではなく じつは10次元とか11次元で成り立っているというものなわけです ここで、疑問に思いますよね!! 1+2+3+‥‥=-1/12 なんで? 1+2+3+‥‥=∞ でしょ? ということです 我々の世界の「数」というのは≪実数≫です 実数とは 正の数(0よりも大きな数。小数や分数を含む) 0(ゼロ) 負の数(0よりも小さな数。小数や分数を含む) のことを言います 実数のうち 小数や分数でもない数が「整数」です 正の整数(1、2、3、4 …) 0(ゼロ) 負の整数(-1、-2、-3、-4 …) を言います 正の整数を、自然数とも言います 実数のうち 1/2とか、1/3とか 分数であらわさられる数を「有理数」といいます 以上の「数」に、ピタゴラスと無理数 で述べた 「無理数」が加わり 実在するすべての数である「実数」とされています こうした「実数」(すべての数)の他に 現実には存在しない「虚数」というのがあります 虚数とは、2乗したときに0未満の実数になる数です 虚数単位は「i」で、i×i=-1 i^2=-1 です 〔2i は、2×iでなく、2や-2と一緒で1つの虚数を表わしています〕 実数+虚数の組み合わせで表す数を 「複素数」(ふくそすう)と言います 例えば (4+2i)×i という複素数と虚数の掛け算を考えます 4×i=4i と 2i×i=-2 との和なので、-2+4i になります 虚数が、現実に存在しない数なので 虚数を含む複素数も、現実には存在しない数です 但し、アルゴリズムと人工知能を教えておられる 知り合いの教授が言うには ≪ 虚数を「存在しない数」と教える人が多いのですが 歴史的にはともかく、また一般の人がそういうのはともかく 専門家が、そう教えていることには猛烈に反論したい それを言ったら負の数だって存在しない数です 負の数に意味を持たせることで存在する数になっただけです 例えば、二時間前と二時間後を区別するために 負の数が有用なので存在するだけです 必要なければどちらも二時間でしかないのです ≫ とのことです なお、アルゴリズムや人工知能で、虚数を使うことはないといいます そもそも情報分野は 離散数学(整数をメインで扱う数学)からなっているからだそうです
3+2i が、複素数です 虚数、複素数を使うことで 1つの数で、座標での位置を表すことができます 〔3+2i は、3とか2とかと一緒で、これで1つの数を表わしています〕 電気回路の交流回路において 電圧・電流を求める計算に 虚数が、実際に使われています 虚数を使うことで、微積分を用いずに 四則演算(足し算・引き算・掛け算・割り算) のみで計算できるようになるからです 例えば、交流回路にコイルがあると 電圧波形に対して、電流波形は90度遅れて発生します  波(山+谷)1つ分が360度 要するに、交流回路で虚数を使うのは 二乗するとマイナスになるという性質が 電圧と電流、電界と磁界の 90度の位相差(ズレ)と一致するからです なお、この電界と磁界が交互に発生し、空間を伝っていくのが電磁波です ある数字(x)を決める(入力する)と それに対応してある数字(y)が決まる式を「関数」といいます 例えば、y=2×x という関数では (2は、1人に配るりんごの数) 人数(x)が決まる 2人(x)➝4個(y) 3人(x)➝6個(y) というように 配るのに必要なりんごの数(y)が決まります また、このとき ≪yはxの関数である≫と表現されます y=2×x は f(x)=2×x と書くこともできることが定められています 1+2+3+‥‥=-1/12 というのは ある複素関数〔二つの複素数があって 一方の値が定まればそれに伴って他方が定まるような式〕 の定義域を広げた関数をつくること これを「解析接続」といいますが それによって、導き出されているのです 但し、1+2+3+‥‥=-1/12 は、騙し式で ζ(-1)=-1/12 が、正しいようです (解析接続をした後は、1+2+3+‥‥ではなくなっている) 物理や化学、天文学といった 自然科学の真理の場合、間違えもあります しかし、数学は、数学自身が研究対象の学問なので 証明された真理(数式)は、数学上、絶対に「正しい」のです つまり、ζ(-1)=-1/12 も、間違えはないということです さて、1+2+3+‥‥=-1/12 の証明に関して 数学者が扱うような解析接続を用いる前段階として 一般の者が理解する分には問題ないという レベルの証明がネットでよくみられます 今回、そのレベルにおける証明に対する間違え証明を 前述のアルゴリズムの教授にしてもらいました ≪ ネットでは、どのブログや動画も いきなり無限の系列を扱っていたので An や Bn が出てくることはないようです (だから、場合分けも出てこなかった) でも、無限和を通常通りの方法で求めるなら An や Bn をまず考えなければならないはずです ≫ とのことでした 〔 An や Bn は、初項からn項までの和を意味しています An=1+2+3+‥‥+n なら 1(初項)からn項まで足した数が、Anです 〕 A 1+2+3+‥‥=-1/12 の証明 まず、S=1+2+3+‥‥=-1/12 を証明し ②で、この証明の誤りを証明していきます A=1+2+3+‥‥ という数式を仮定し S-A を計算してみます すると 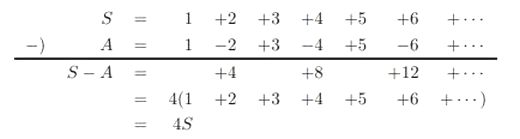 したがって、S-A=4S であるので S=-A/3 となります 〔S-A=4S の両辺からSを引くと -A=3S になるので、 両辺を3で割れば、S=-A/3 になります〕 S=-A/3 となるので A=1/4 が成り立てば、S=-1/12 となります 次に、Aを計算します 下のように一つずらすして、AにAを足してみます 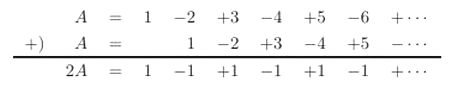 B=1-1+1-1+‥‥ という数式を仮定すると 2A=B すなわち A = B/2 であるので B=1/2 が成立すれば、A=1/4 すなわち S=-A/3=-1/12 が得らます 最後に、B を計算します 下のように一つずらすして、BにBを足してみます 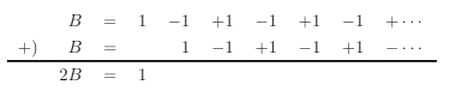 以上のことから B= 1/2 すなわち S=-1/12 が得られました B 1+2+3+‥‥=-1/12 の間違い証明 まず、1+2+3+‥‥ を厳密に書くと lim n→+∞ (1+2+3+‥‥+n) となります lim(リミット )とか n→+∞ というのは 高校の数学で習う「極限」で用いる記号です lim n→+∞ (1+2+3+ ‥‥ +n) というのは、 n が無限大を目指しているという前提のもとで カッコの数式は、なにを目指しているか ということです そこで、Sn=1+2+3+‥‥ +n を、求める必要があります 〔Snは、数式の初項(ここでは1)から、n項までの和を意味する〕 これは、Sn =n(n+1)/2 となります 【 Sn= 1+ 2 + 3+‥‥+ n と Sn= n +(n-1)+(n-2)+‥‥+ 1 とを足すと ( n+1 (n-1)+2=n+1 (n-2)+3=n+1 ・・・・ と足していく ) Sn×2= (n+1) + (n+1) + (n+1) ‥‥+ (n+1) となります (n+1) は n 個あります 要するに Sn×2=n(n+1) となるので Sn=n(n+1)/2 となります 】 以上のことから、n → +∞ のとき (n が無限大を目指しているという前提のもとでは) n(n+1)/2の分子は、どんどん大きくなっていく= n(n+1)/2は無限大に近づいていく=発散します ついでなので、極限とはどういうものなのか 一つ例を書いておきましょう lim_{n→+∞} 2n/(n+1) では 分子 2n も、分母 n+1 もどちらも限りなく 大きくなっていきますが 分子と分母を、それぞれ n で割ると (ある分数式に対して分子分母を同じ数で割っても値は変わらない) 分子は、2n➝ 2 になります 分母を説明すると nをnで割ると1 1をnで割ると1/n です 極限というのは、 nが無限大を目指している という前提のもとでの答えなので n/1は、無限大を目指していることになりますが 1/nだと、限りなく小さい数=0 を目指していることになり 1/n=0 となります なので、 1 + (1/n)=1です それゆえ lim_{n→+∞} 2n/(n+1) =2/1= 2 となります 話を戻します では、①でなぜ、1+2+3+・・・・=-1/12 の証明 が、成り立ったのだろうか? 答えは、誤りの部分を +・・・・ の部分に、巧みに隠して計算しいたからなのです 実際のSnと An =1-2+3-4+・・・・-n (n が偶数のとき) An =1-2+3-4+・・・・+n (n が奇数のとき) Bn=1-1+1-1+・・・・ - 1 (n が偶数のとき) Bn=1-1+1-1+・・・・ + 1 (n が奇数のとき) を用いると、以下のようになります n が偶数のとき 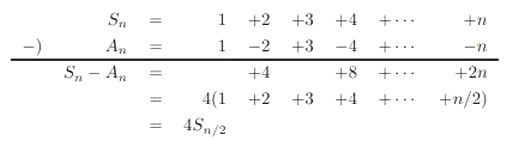 Sn-An=4Sn でなく Sn-An=4Sn/2 が正しいわけです したがって、Sn-An=4Sn すなわち Sn=-An/3 は成立しません 同様に 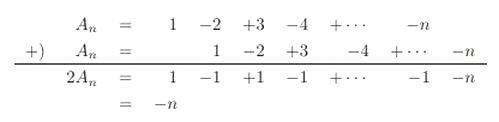 An=-n/2 となり An=1/4 は成立しません 最後に  すなわち Bn= 0 となり Bn=1/2 は成立しません nが奇数のとき、同じ計算をすると  ということです 数学というのは、表現方法(言語)の一つで 表現が可能であれば 真偽を確かめる強な手段となりますが 現実世界で、表現できることは少ない ということなわけです フラクタルの理論について ① 完全数について (ひとつ戻る) |
|