【 数学・物理学 編 】 フラクタルの理論について ① フラクタルとは、1980年代に フランスの数学者 ブノワ・マンデルブロ(1924~2010) により提唱された複雑な図形です 以下の2つの性質をもつとされます 1、自己相似 図形全体(自分)の中に、相似な形(自分と同じ小さな形)を含む 2、三角形なら辺の長さ、円なら半径の長さで特徴づけられているが そうした図形と違い、長さで特徴づけることができない フラクタルはいくつかあるようですが とくに知られているのが、コッホ曲線と シェルピンスキーのギャスケットです シェルピンスキーのギャスケットの ギャスケットとは水道管とかとかで使うゴムパッキンのことらしく シェルピンスキーの三角形ともいいます
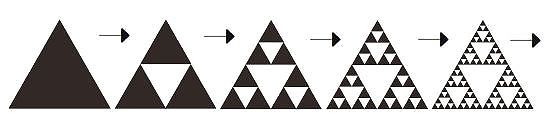 ポーランドの数学者のシェルピンスキー(1882~1969)が 発表したフラクタルで、シェルピンスキーのカーペットも知られます
コッホ曲線は、スウェーデンの数学者 ヘルゲ・フォン・コッホ(1870~1924)が考案したフラクタルです 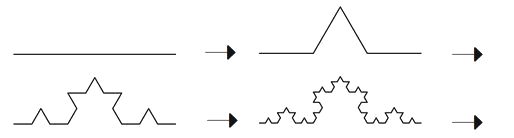 線を三等分し、その真ん中の線を1辺とする 正三角形を作っていくことを繰り返します この操作を無限回数 繰り返すとコッホ曲線になるとされます 無限回 繰り返すと、もはや直線でできた図形としては複雑すぎる ということで曲線というそうです  これは、カントール集合と呼ばれるフラクタルです 1874年にイギリスの数学者 ヘンリー・ジョン・スティーヴン・スミス により発見され 1883年に、集合論をつくったドイツの数学者 ゲオルク・カントール(1845~1918年)によって紹介されたといいます 3等分した真中を抜くという操作を 無限回繰り返した図形が、カントール集合(カントールの三進集合)です 自然界では、天の川、雲、樹木、シダの葉 血管の分岐構造、リアス式海岸などが フラクタル構造をもっているとされています
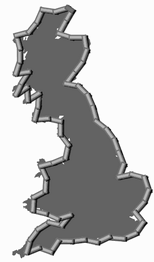
ロマネスコ(右)は、カリフラワーやブロッコリーの仲間で 野菜として食べられている フラクタルの発見は、イギリスの気象学者 ルイス・フライ・リチャードソン(1881~1953)だといいます 彼は、国境を接するスペインとポルトガルが 国境線について、それぞれ別の値を主張していたことから 国境線の長さは、用いる地図の縮尺によって 変化することを発見したといいます このような特徴をフラクタルと名付けて リチャードソンの示した「海岸線のパラドックス」を拡張したのが マンデルブロだといいます 海岸線のパラドックスとは 海岸線の長さが、フラクタル的性質をもつため 1つに確定しないというものです
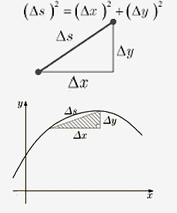
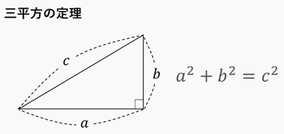
海岸線を測るとき、定規の長きが長いと 入り組んだ場所は測れません 正確に測るためには、短い定規を使う必要がありますが 短い定規でより正確に測ると、その分、海岸線の長さが長くなります 正確に測れば、測るほど、海岸線は長くなります 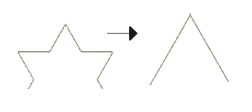 ふつうの図形の場合、拡大すると ギザギザ度、デコボコ度は、小さくなっていきます 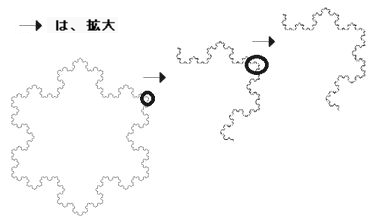 フラクタルは、自己相似という性質をもつので どんなに拡大しても、ギザギザ度、デコボコ度は一緒です 曲線の長さを測るには、地図を拡大し 積分法と、三平方の定理を用いれば いいわけですが
海岸線は、コッホ曲線に類似していて 無限にギザギザしているので、長さは無限となり測定できない というのがこのパラドックスです マンデルブロ集合は マンデルブロによって提唱された複素数の集合で どんなに拡大しても次々に最初と同じ形が現れる図形です 〔2乗したときに0未満の実数になる数を 虚数といい 実数+虚数の組み合わせで表す数を 「複素数」(ふくそすう)という〕  黒い部分がマンデルブロ集合にあたり 周囲がカラフルなのは 集合に属さない点を発散速度によって色分けしているからだそうです 発散速度というのは、n➝∞ (nが無限を目指しているとき)の 無限に近づいていくスピードのことで nよりもnの2乗のほうが、当然、発散速度は速いです nが1だと、nの2乗は2ですが nが100になると、nの2乗は2の10の30乗ぐらいになります 学校で習うきちんとした図形、丸とか三角や四角とかいった図形に 限定された幾何学だけでは、複雑な自然界の形状を解明することはできない そこで、従来の幾何学(ユークリッド幾何学)に追加された新しい幾何学が フラクタル幾何学である というのが、マンデルブロの主張のようです マンデルブロは「自然はフラクタルである」という言葉を残しています 自然の形成原理は「自己相似性」にあり 複雑に見える自然も、シンプルなパターンの連続で成り立っている 簡単な式が繰り返されことで、複雑さを形成している ということらしいです 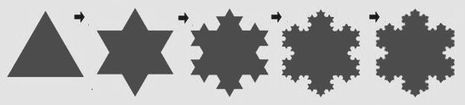 各辺で、コッホ曲線の操作をし、無限回の操作で、コッホ雪片となる
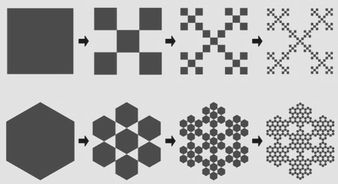
下の図形の抜けた部分は、三角→六芒星→コッホ雪片 になっています また、自己相似性に ちょっとランダム(不確定要素)が加えると、カオスが現れるといいます 樹木、シダの葉、リアス式海岸などを 例にとって言い過ぎじゃないのか と思われますが(笑) 密教の曼荼羅と関連づけて フラクタル理論は、宇宙の構造原理を明かしたものであるとか 進化のツリーもフラクタルであるとか 時間においては、「部分」が「全体」を表すということから 一瞬の中に、一生が存在するとか ヒトの一生に、宇宙の一生が凝縮しているとか 様々な分野で、色々なことが語られています
チベット仏教の 身口意具足時輪(カーラチャクラ)曼荼羅
但し、フラクタルというのは 理論的には、仏教でいうと、宇宙の根本仏である 大日如来との一体化を目指す密教よりも 華厳宗の「一即一切・一切即一」の考えに近いです 華厳教学の根本は 「法界無尽縁起」(ほっかいむじんえんぎ・ あらゆる事物が互いに縁となり 自在に限りなく交流、融合しあって生起している) 「相即相入」(そうそくそうにゅう・対立するように見えるが 両者の間に本来 差はなく、とけあい影響し合う) 「主伴無尽」(しゅばんむじん・一切が無限に主体となり 伴(客体・従属)となり、しかも互いに矛盾なく関係し合いさしさわりがない) 「重重無尽」(じゅうじゅうむじん・ 全ての存在が互いに関係し合って尽きることがない 中央に火を置き、周囲を鏡で囲むと鏡に火が映り それがさらに他の鏡に映り幾重にもなるなどと譬える) 「一即一切・一切即一」(1個と全体とは本来全く同じ存在である) といったところです つまり、≪形状の一即一切・一切即一≫が フラクタルであって 部分を分解してみても、そこにまた無限が出現する そこでさらに小さく分解しても そこにもまた無限が出現するといった話なのです コッホ曲線は、無限の長さをもっていて 測定を完遂できないという話は 古代ギリシアの自然哲学者 ゼノン(前490~前430頃)の 「アキレスと亀のパラドックス」に似ています まず「アキレスと亀のパラドックス」を書いておきます アキレス(ギリシア神話に登場する英雄) と亀が競争しました アキレスにはハンデを負わせ 亀のスタートするA地点より 後ろのB地点からスタートさせます 1人と1匹は同時にスタートします アキレスの速度を亀の2倍とします AからBの距離を1とします するとアキレスがAに到着したときには 亀はそこから1/2進んでいる 次にアキレスが亀のいた1/2地点に到着すると 亀はアキレスより1/4進んでいる アキレスが1/4地点に着くと、亀はそこから1/8先にいる‥‥ こうしてアキレスは永遠に亀に追いつくことができない といったものです じつは、亀が与えられたハンデの距離が1で アキレスの速度が亀の2倍だから 亀が1進んだらアキレスは追いつくことができます ですが、亀の進む距離が 1/2+1/4+1/8+1/16+1/32+1/64+1/128‥‥で この計算方式だと1になることはないのです 【 亀の進む距離… 1/2(2/4)+1/4=3/4 3/4(6/8)+1/8=7/8 7/8(14/16)+1/16=15/16 15/16(30/32)+1/32=31/32 31/32(62/64)+1/64=63/64 63/64(126/128)+1/128=127/128 127/128(254/256)+1/256=255/256 】 これを時間で、説明すると アキレスが秒速1m・亀が秒速0.1m アキレスはA地点から、亀はB地点からスタートします スタートから1.9秒後 アキレスは1.9m地点(B) 亀は1.99m地点(C)にいる スタートから1.99秒後 アキレスは1.99m地点(C) 亀は1.999m地点(D)にいる スタートから1.999秒後 アキレスは1.999m地点(D) 亀は1.9999m地点(E)にいる ということになり アキレスが、亀に追いつこうとする行為は 1.999999‥‥秒後と 無限に繰り返すことができます しかし、本質的には、スタートから2秒後には アキレスは、亀に追いくことができます 数学においては、この事実をもって 「アキレスと亀」は 「無限の回数を繰り返せる」ことと 「無限の時間かけても追いつかない」こととを 混同するところから生まれているパラドックスである 「回数の無限」と 「時間や距離の無限」とを 混同するところから生まれているパラドックスである という反証がなされます つまり、「アキレスと亀のパラドックス」の場合 有限を、無限に刻んでいるだけで ホントの無限ではないということです 「海岸線のパラドックス」というのも一緒で 海岸線を正確に測ることができない というのは、正確に測る方法がないというだけの話であって ホントの無限ではないのでは? という疑問が生じますよね コッホ曲線というのは 正三角形をつくる操作がなされるたびに 1辺ずつ増えて(長さが増えて)いって 無限回繰り返し、完了すると コッホ曲線として完成するとされ このときの長さは、無限大とされています  (A→Bの直線距離は同じです) そもそも直線だって、おもいっきり拡大すると ギザギザしているし、でこぼこしていますよ(笑) 原理的には、直線も、海岸線も一緒という話にもなります 直線がちゃんと測れないわけですから 三角形も、四角形も、円も ≪完全に測る≫なんてムリなのです こうした疑問を解決するために 知り合いのアルゴリズムと人工知能の教授に 「海岸線のパラドックス」についての考えをいただきました ちなみに、私は凡人ですが この教授は、半端ない (笑) こんな↓メールいただきました 東大2020年度前期入試の数学(理系)を解いてみました 笑 #要するに、今年の2月に行われた入試問題! 結果は、ものの2時間で最後の第6問の小問1つを除いて 全部解いてしまいました この歳になっても、まだまだ解くスピードはあるようです (^^ゞ #実際の制限時間は、2時間半で大問が6問です 念のために言っておくと、普段使わない数学の道具もあるので 久々に接した問題も当然ありました 昔はもっと難しかったと思っているのですが この問題なら理3の合格者なら全部取れてもいいだろと思うのですが 〔 理科三類は、東大生の中でも 住む世界が違うと言われている 東大合格者約3000人のうち100人程度 日本の1世代あたりの人口を100万人強として計算すると 同世代の0.01%しか入学できないといいます〕 これでも去年より難しいというから 昨年度はどれだけ簡単だったんだ?と不思議に思っています 残った最後の小問はちゃんと紙と鉛筆を持たないと難しそうなので 明日、机の上で格闘する予定 #それ以外は片手間でメモ程度で片づけました (^^)v 最後に残っていた問題、終わっちゃいました ちゃんと紙と鉛筆があるとやっぱり楽ですね もっと苦戦するかと思っていたのですが 思いのほか簡単でした 昨日、解くスピードの観点で私もまだまだと言いましたが 「時間をかけさえすれば当然解ける」と暗に発言してました (^^ゞ 研究者は基本的にしつこいので 食いついた問題は解けるまで時間をかける発想になっているのです 困った人種です 笑 まず、パラドックスについておさらいします 【 ある島の海岸線を、長さ1kmの定規で測ったところ 定規が5本分の長さでした なので、海岸線の長さは 1km×5=5km です ただ、定規が長かったので 海岸が入り組んでいる場所は測れませんでした もう少し正確に測るために、0.5km の定規を使ってみました すると、海岸線の長さは定規16本分 0.5km×16=8km となりました 1kmの定規で測ったときより、海岸線が3km 長くなりました さらに定規の長さを短くして測ると、海岸線はさらに長くなりました 地図を拡大していくと、見えていなかった細かいデコボコが見えてきます それをもっと短い定規で、正確に測ると、さらに海岸線は長くなりました いくらでも拡大していくことができるので 海岸線は、果てしなく伸びていき、長さは、無限大になってしまう 】 教授の解答を記します 単なるパラドックスの話なので 真面目に考えない方がいいですよ と言いたいところですが、笑 スッキリしないと思うので 何がおかしいのかをお話ししておきます 海岸線を長い定規で測るとします 定規は直線ですが、海岸線は曲線です ですので、曲線を無視して定規で測ると 実際の距離より短くなります では、定規の長さを短くします 先ほどよりは小回りが利くので 測定結果は実際の曲線に長さに近づき 長くなります さらに定規の長さを短くします さらに小回りが利くので さらに測定結果は先ほどより長くなります 海岸線はどこまで細かく見ても曲線なので 定規の長さを短くし続ければ 測定結果は長くなり続ける 測定結果が長くなり続けるということは 海岸線の長さは無限ではないか? と言うのが「海岸線のパラドックス」の主張です このパラドックスは 測れないから無限大と言っているわけではなくて 定規の長さを短くすれば測定結果が長くなるから 定規の長さを(0にならないようにして) 永遠に短くし続ければ 測定結果も永遠に長くなり続ける=長さは無限である という主張です このパラドックスの誤りは 測定結果も永遠に長くなり続ける=長さは無限である にあります # そもそも、定規の長さを永遠に短くし続けなければならない 海岸が存在するのかという話もありますが 笑 先ほどの例ですが 最初は5km、次は3km 長くなっわけですが 定規を短くするのが n 回目のときに 長さが前回測定結果より 5× 0.6^n だけ増えるとします 0.6^n とは 0.6 の n 乗 すなわち、0.6 を n 回かけた数です 要するに、最初は 5km で 次に 5×0.6=3km 長くなって その次は 3×0.6=1.8km 長くなって さらに 1.8×0.6=1.08km 長くなり 1.08×0.6=0.648km 長くなり… と永遠に繰り返したとします これを繰り返すと 確かに永遠に測定結果は長くなり続けるのですが 無限に続けても 5÷(1-0.6)=12.5km にしかならないことが 計算できます 要するに 5×(1+0.6+0.6^2+0.6^3+ …)=12.5 となります つまり、無限に足し続けたからといって 足した結果が無限になるとは限らないのです それが今回のパラドックスの正体です # アキレスと亀のパラドックス と本質的に変わらないのです 【 5÷(1-0.6)=12.5km について 最初の長さが 5km 次に、長さが 5×0.6km=3km 増える 次に、5+3=8km から 長さが 5×0.6^2=1.8km 増える 次に、8+1.8=9.8km から 長さが 5×0.6^3=1.08km 増える・・・・ とします 5km から (n-1)回まで長さが増えたときの合計の長さをLnとします Ln=5+(5×0.6)+(5×0.6^2 )+ … +(5×0.6^{n-1}) これは、初項 a=5、 公比 r=0.6 の等比数列の和になっています この式の和は簡単に求められ、公式にもなっていますが ちゃんと求め方を書いておきます Lnを 0.6倍すると 0.6×Ln=(5×0.6)+(5×0.6^2)+ … + (5×0.6^{n-1})+(5×0.6^n) となります 0.6^n とは 0.6 の n 乗 すなわち、0.6 を n 回かけた数です 5を0.6倍すると、(5×0.6) (5×0.6)を0.6倍すると、(5×0.6^2) (5×0.6^{n-1})を0.6倍すると、(5×0.6^n) となります Lnから 0.6×Lnを引くと Ln= 5+(5×0.6)+(5×0.6^2)+ … +(5×0.6^{n-1}) 0.6×Ln=(5×0.6)+(5×0.6^2)+ … +(5×0.6^{n-1})+(5×0.6^n) 共通の部分がなくなって Ln-(0.6×Ln)は、5-(5×0.6^n) となります つまり、Ln-(0.6×Ln)=5-(5×0.6^n) です 左辺をLn でくくると (1-0.6)×Ln になります 右辺を5 でくくると 5×(1-0.6^n) になるので (1-0.6)×Ln=5×(1-0.6^n) さらに、Ln=5×(1-0.6^n)÷(1-0.6) となります これでn を大きくしていくと 0.6^n は、0に近づきます 0.6×0.6=0.36 0.36×0.6=0.216 0.216×0.6= ・・・・ これを繰り返すと 0 に近づくのがわかると思います n が無限のとき、0.6^n=0 なので n が無限ならば Ln=5×(1-0.6^n)÷(1-0.6) は Ln=5×(1-0)÷(1-0.6) Ln=5×(1)÷×(0.4)=25/2=12.5 になるわけです 】 つぎに、コッホ雪片についての面積について 聞いてみました 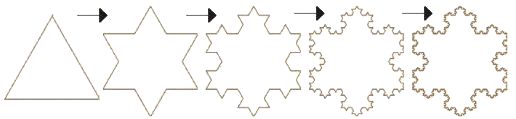 ➝ の操作を無限回繰り返し、完了した雪の結晶のような図形が 「コッホ雪片」とされます コッホ曲線というのは 正三角形をつくる操作がなされるたびに 1辺ずつ増えて(長さが増えて)いきます 線分が無限に増えていくとしたら 面積も無限に増えていくはずですが コッホ雪片は、長さは無限で、面積は有限とされます 仮に、無限大の長さが存在するとしたなら 面積は有限になるということなのでしょうか? 教授の解答を記します 相似な図形であれば、線が長くなれば面積が増えますが 線の長さと線で囲まれた面積は必ずしも関係がないです 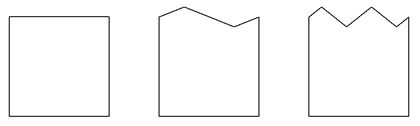 例えば、一辺が10cm の正方形があったとします そのうちの一辺だけをジグザグに変えるとします 例えば、上に1㎝ 下に1㎝ にジグザグを繰り返すのが 1往復のとき、2往復のとき、3往復のとき... と増やすと、長さは長くなっていきます しかし、面積は全く変わらないのです 凸と凹が繰り返されるだけだからです 面積が無限になるということは どれだけ大きな面積を持つ紙を用意しても 線分を_∧_に置き換える操作を何度も繰り返すと そのうちに用意した紙に書けなくなるということなので それが起こらなければ面積は有限ということになります コッホ雪片は確かに面積が有限みたいです そもそもコッホ雪片は 図形全体(自分)の中に、相似な形(自分と同じ小さな形)を含む という「自己相似」をもたないですよね と聞くと 厳密には自己相似を持たないです Wikipediaでフラクタルを確認しましたが どうも定義が揺れてる概念みたいですね 「自己相似を持つ」は提案されている定義の一つみたいです 感覚的には研究者の間で共通認識があるけれど それを数学的に上手く表現できていないみたいです ここからは私の勝手な解釈ですけど フラクタルとはどれだけ拡大しても複雑である線 を言っているみたいです その意味でコッホ雪片はフラクタルなんでしょう 定義って難しいんですよね 苦笑 フラクタルの理論について ② 数学の空間次元と 超弦理論の次元の式 (ひとつ戻る) |
|






.jpg)
11.jpg)


