【 数学・物理学 編 】 ① 現代数学とはなに? 数学とは、世界を数で定義する学問と言えますか? という質問を、知り合いのアルゴリズムの教授にしてみました 例えば、0より小さい数が考えられるようになり 「今日は、昨日よりも気温がマイナス2℃だった」 という表現が可能になった という意味は 水の氷る温度を0℃と決めて 負の数を用いることで、温度(熱)という世界を定義していますよね すると、数学とは、一種の自然科学と 言えなくもなさそうですが 数学には、単に、数学自身を 研究対象とされている場合もありますか? 教授の答えはこうです 現代数学は数学自身が研究対象で、それ以外の動機はないと思います 但し、そういった「何の役にも立たない」はずの数学が 「後になって」何かの現象を説明することはよくあります それから、高校までで扱っている数学については おそらく全て他分野の必要で出てきたもので 色んな現象を説明するための道具だったのは間違いありません ですので、割と最近まで自然科学の一分野だったはずです (あくまで私の認識ですが) さらに、以下の質問をしてみました 現代数学とは 結局なんなのですか? ネットで調べてもよくわかりません みんな概略を述べないで色々書いているだけなので・・・ ネットで、このよう↓に書いている方がいます ≪それまでの近代の数学の中心は、微分積分であったが 現代の数学というのは、かなり新しい考え方をするもので 大学の数学科に進学した人以外は馴染みが薄いもの≫ ≪近代までの数学を忘れてしまった方がよいくらいに 別な考え方をしているもの≫ ≪20世紀になって登場した数学である≫ しかし、別の人は 古典数学と、現代数学に分けて 微分積分を、現代数学の代表格であるように書いています また、≪古典物理と現代物理のように はっきりと分けられてはいないように思う≫ ≪強いて言えば、近代数学とは 集合論を基礎に、公理化を徹底的に勧めた ブルバキからではないだろうか?≫と書いている方もいました 教授の答えは、明快です ≪現代数学の代表格である微分積分≫ これは嘘ですね 微分積分学はニュートンの時代には かなり体系化されているので 完全に古典~近代の部類に入ります 要するに現代ではないです #古典と近代の区別は分からないので 私はまとめて古典と呼びたいのですが 現代数学については 最初の方の言い分の方が正しいと思います 私の感覚でも20世紀以降の数学を現代数学と見ています ブルバキという(架空の)人物が出てきていますが ブルバキによる『 数学原論 』を現代数学の出発点と見なすのは 一つの考え方です #ブルバギは、複数の数学者によるグループです (主にフランスの若手の数学者集団のペンネーム) 分かりやすく言うと 公理(定義)と、推論規則を厳密に定めて 議論する方向にシフトしたのが、ブルバキの『数学原論』です 例えば、我々は2次元座標(x, y座標)上の直線を 中学校で習うことになりますが x, y座標って何?って聞かれると 正しく答えることは難しいと思います 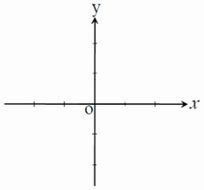 多分、直角に交わった2つの直線があって… となるかと思いますが 直線や直角はこの時点では定義されていません というか どちらもx, y座標が定義されてから初めて定義されるべきものなので x, y座標の定義に直線や直角は使ってはいけません このようにこれまで習ってきた数学の中には 実は直感的な定義というものが案外あるものなのです 古典数学の中でもこういうものは曖昧にされてきていたのですが 定義があいまいだと結論もあいまいにならざるを得ない それを嫌って定義(と推論規則)を厳密にしたのがブルバキです 【 公理とは、数学の理論をつくるとき 基礎におかれる命題(主張)であり 平行線は交わらないとか 三角形の内角の和は180度とかいったもの 証明を必要としない基礎的な原則で、無証明命題ともいう 真であると仮定されたもの(論理式)が、公理 真であると証明されたもの(論理式)が、定理 推論規則は、定理から別の定理を導くルール 】 ブルバキの仕事には重要な点があって 数学内でモデルを構築して議論をすることが可能になったことです そのモデルが現実にないものであったとしても 公理(定義)と推論規則が整えばそれでモデルになるので 自然科学から離れた数学独自の問題を 扱えるようになった点は大きいと思います 現代数学でもブルバキのスタンスは踏襲されているので ブルバギ以降を現代数学と呼ぶのは一つの考え方だと思います 起点をブルバキとするのは 一つの考え方ということですか? 私は決して数学の専門家ではないので 何をもって現代数学と呼ぶかを決める立場にはありません かと言って、何をもって現代数学と呼んでいるを 専門家の立場で説明してくれている文献(webを含む)もありません (見つけられていないだけかもしれませんが) ですので、あくまで私の印象という域を出ないので 言葉を濁しています ただ、現代数学のとらえ方として 大きく間違っているとも思っていませんが・・・ じつはブルバキ以外にも思い浮かぶ人物は一人います ヒルベルトという人物です こちらは実在の人物です ヒルベルト・プログラムというのがあるのですが これを起点に考える方がいいのかもしれません と思って調べたところ 彼が「現代数学の父」と呼ばれているそうです これで少なくとも起点はハッキリしました #「現代数学の祖」や もう一人の「現代数学の父」が現れない限りは 笑 ブルバキの数学原論と目的は違うようですが 数学を公理と推論規則からなるものとして 形式化して考えるという点では同じことを考えています ちなみに、ヒルベルトが活躍したのが ちょうど1900年頃なので私が感覚的に言っていた 「現代数学=20世紀以降の数学」とも合致します それと私が説明しようとしていたのは 「形式主義」と言うのだそうです ということでした 形式主義を、ウィキペディアで調べてみると ヒルベルト(1862~1943・ドイツの数学者)によって主張された 【 数学は決められたルール (公理と推論法則)に従って行われるゲームであり ルールを取り替えることによってできる異なるゲームは それぞれ同等である 】 という考え とありました つまり、大学から勉強する数学は あるルールのもとになされるゲームにすぎす ゲームに真理も虚偽もないのと一緒で 現代数学の数式が、現実世界の真理を表わしている わけではないということです 20世紀最大の哲学者と称される ウィトゲンシュタインは 我々の世界は「言語ゲームである」と述べましたが 現代科学というものも、数字と数式という言葉による 言語ゲームにすぎないということです ② ヒルベルトプログラムと ゲーデルショック カントール(1845~1918・ドイツで活躍した数学者 によって 「集合論」と呼ばれる数学の分野が発明されました この集合論は、集合という概念だけで あらゆる数学の概念を説明できる理論であり 現代数学にとてつもない影響を及ぼしているといいます ところが、しばらくすると バーランド・ラッセル〔1872~1970・イギリスの論理学者 数学者、哲学者。ノーベル文学賞を受賞〕によって 「ラッセルのパラドックス」が明らかになります ある村に、自分でひげをそらない人全員の ひげをそる床屋がいました そうすると、この床屋自身のひげは誰がそるのでしょうか もし、床屋が自分のひげを自分でそるとすれば この床屋は、自分でひげをそらない人の ひげをそるのだから矛盾する そこで、床屋が自分のひげはそらないとすると この床屋は自分自身のひげをそらない人全員の ひげをそってやるのだから これも矛盾する どちらにしても矛盾してしまう この「床屋のパラドックス」は 「ラッセルのパラドックス」を分かり易く説明したもので 集合には 赤くないものの集合(A)のように 「自分(集合)自身をその要素として含む集合」 (集合自身は赤いものではない)と 赤いものの集合(B)のように 「自分(集合)自身をその要素として含まない集合」 があり 集合の集合であるCをどちらに含めても 矛盾が生じるというのがラッセルのパラドックスだそうです 例えば 世界のあらゆる図書を あらすじからAのグループに入る図書と Bのグループに入る図書に分けた グループAは自分(その本自身)について書かれている本 グループBは自分について書かれていない本である Bの目録として、新たにTという本が作られた Tは図書だから、AかBのいずれかに属するはずである Tは目録なので自分について書かれていない なのでAには属さない そこで、TはB(自分について書かれていないグループ)に 属すると仮定する すると、Tは、グループBに属するとともに グループBの目録ということになる ならば、Tは、T(自分)について書かれている本になる グループBは、自分について書かれていないグループなので ここに矛盾が生じる したがって「現存する全ての図書について 記載した図書目録は存在しない」ことになります 集合論によって、数学の全てが説明できるわけですから 集合論の矛盾はそのまま数学の矛盾ということになります そこで、現代数学の父と呼ばれる ヒルベルト(1862~1943・ドイツの数学者)は 集合論の公理系(公理の集まり)を整備し 完全性(全てが証明あるいは反証できる)と 無矛盾性(どのような推論に対しても、決して矛盾が導かれない)とを 実現しようと、数学者たちに呼びかけました これが「ヒルベルト・プログラム」です これには、数学の危機を救おうと多くの数学者たちが参加したそうです ところが、そんな中、クルト・ゲーデル(1906~1978・ オーストリア・ハンガリー帝国出身の数学者)が 「不完全性定理」を証明しまったのです 不完全性定理には 第一不完全性定理と第二不完全性定理があって 第一不完全性定理は 公理系の表現力が一定以上となった場合 完全性と無矛盾性とは両立しないというものだそうです 具体的には、ゲーデル数というものを用いて ある条件を満たす自然数論においては、どんな工夫をしても 「自己言及のパラドックス」が生じることを証明したといいます 「自己言及のパラドックス」と 前述の「床屋のパラドックス」とは 概念という広い意味においては、同質です パラドックスの最も基本的なものとして 古代ギリシャの哲学者 エウブリデス(紀元前4世紀頃・アリストテレスと同時代の人) が作ったとされる「嘘つきのパラドックス」 (自己言及のパラドックス)が知られています ある男が「私が今言っていることは嘘だ」と言った この言葉が「真」なら、彼は嘘をついていることになる この言葉が「偽」なら、彼は本当のことを言っていることになる したがって、男が嘘をついているなら彼は真実を述べている 男が本当のこと言っているなら彼は嘘を言っている という逆説です 第二不完全性定理では 第一不完全性定理で示される 「証明も反証もできない命題」の一例が 自分自身の無矛盾性を表す命題であることを証明しています 要するに、論理式 f が、 f 自身の無矛盾性を表現している場合 f を、証明も反証も出来ないということです 「私が今言っていることは嘘だ」を 証明も反証も出来ないということです この不完全性定理は 「数学を基礎にした自然科学によって、世界の全てに答えを出せる」 と信じていた数学界に 「ゲーデルショック」と呼ばれるほど、大きな衝撃を与えたといいます ≪数学の真理を積み重ねていけば いつかは神の真理にたどりつけるはずだ≫ という信仰を、根底から崩壊させ 数学者たちに「数学は考えていたほど万能ではなかった」 ということを悟らせるに至ったのです まとめると ゲーデルの不完全性定理とは 「どれだけ正しい数学を確立したとしても その数学の内部に正しいとも誤っているとも証明できない 命題が存在する」ということです この定理の肝は、証明できない命題が 確立されている数学の体系の内部に存在するということ さらには、 どのような数学の体系であっても存在するということです そこで「数学で世界を表現することはできるのか?」 ということになると ゲーデルの不完全性定理だけでは 「数学で世界を表現することができない」 という話にはならないのですが 不完全性定理によって ≪世界を説明しうる 新しい数学が発見されたとしても 説明できない世界の部分が残り続ける≫ ということは言えます 少なくともその可能性が考えられるということです 自然科学の証明と数学の証明 ピタゴラスと無理数 (ひとつ戻る) |
|