【 数学・物理学 編 】 フラクタルの理論について ② 最後にいよいよ核心の質問をしてみました 海岸線が、仮にコッホ曲線だったら長さは無限ですか? 教授の解答を記します アレフ0の「無限」というのは どんな数を持ってきても、それより大きい数が存在する 有限に抑えることができない という意味での無限です (アレフ0の集合を対象とする数学を、離散数学という 簡単にいうと、整数をメインとして扱う数学のこと) コッホ曲線の各線分___を _∧_ に置き換える操作を 無限回数行うと言いいますが、そもそも無限という数はないのです 「終わりがない」ことをそう呼んでいると考えた方が近いです ですので、置き換え操作を無限回数行うと 長さが無限になると言っていますが 正しくは ≪置き換え操作をくり返し続ければ 長さも長くなり続ける≫というのが正しいです 海岸線が、コッホ曲線だとすると 与えられた長さまで測ると 後出しじゃんけんのように、新な長さが次々に つくられていくという話になりますが 海岸線は別に自力でコッホ曲線の置き換え操作を 行っているわけではないので どこかで、後出しじゃんけんができなくなります くり返しに限りが来ます 無限にはなりえないのです 要するに、海岸線は操作回数が固定されたコッホ曲線です 長さを測定する側が コッホ曲線に合わせた小さな定規を持ち込むことで 長さが確定してしまうはずです 緋山: 「無限にギザギザしている図形(フラクタル)は 自己相似なので どんなに細かく分解して無限に ギザギザしている」 という話を 有名な数学・物理の教育系ユーチューバーのヨビノリさんが 動画でしていますが これについてはどうですか? 教授: 実際に無限にギザギザしている図形なんて存在しませんよ まあ、仮に電子や陽子とか もっと細かい物理の最小単位のレベルで フラクタルになっていると仮定してもいいですけど 結局そこで終わりって話です フラクタルの長さについては 「操作を無限回 行う」というところに 怪しさが隠されていると思えます 無限の乱用があるように思えます 緋山: 【 海岸線は別に自力でコッホ曲線の置き換え操作を 行っているわけではないので どこかで、後出しじゃんけんができなくなります くり返しに限りが来ます 無限にはなりえないのです 】というのは 置き換え操作を行っている人間が有限の存在だから という意味ですか? 教授: わたしが、置き換えを無限に行えないと言ったのは 物理的な限界のためです 海岸線は、(一部の)人間が、勝手に フラクタル(コッホ曲線)だ と言っているだけですが コッホ曲線も同じです 置き換え規則を繰り返すと 線分が、限りなく小さく(短く)なります こんな風に考えてみて下さい 野球ボールを並べて 1cm単位の折れ線を作ることができますか? もちろん答えは NO ですよね 置き換え操作を繰り返すと 線分の長さが 1cmどころか 1mm, 1μm, ... といくらでも小さくなっていきます それを野球ボールで構成することは不可能です 野球ボールを原子に置き換えても一緒です ならば、表せる線分の長さにどこかで限界がやってくるのです 無限にランクがある? 数学の集合論では、無限にもランクがあり アレフ0、アレフ1、アレフ2・・・・と、呼ばれています アレフは、無限集合の濃度(あるいは大きさ)を示す単位です 自然数は、1、2、3、4、5・・・・と、無限個あります 奇数は、1、3、5、7、9・・・・と、無限個あります 自然数と奇数はどちらが多いでしょうか? 有限なグループで考えれば もちろん自然数の方が、奇数よりも2倍多いですが 無限なグループで考えれば、数は一緒です 実数の場合、0と1の間を埋めるのに 100等分、1000等分、10000等分・・・・ とどこまでも間隔を狭めることができます これに対して、整数の場合、間を埋めることができません これが、実数の連続性であり 整数の離散性(とびひびの値を示す性格)です そして、自然数も、奇数も とびとびの間隔=濃度 が一緒なのです 濃度が一緒ということは 1つ1つの数字が「一対一対応」である ということです なので、無限なグループで考えれば 自然数も、奇数も、数は一緒なのです ≪無限個なら、どんな無限個も同じである≫ この従来の数学者の考えに対し 集合論を確立した カントール(1845~1918・ドイツで活躍した数学者)は 「そうではない 無限にも濃度がある」と主張したわけです そして、自然数の持つ濃度のことを「アレフ0」と名付けました 自然数の方は「離散」(とびとび)で、実数の方は「連続」です では、実数の無限集合は、アレフ1なのでしょうか? じつは、自然数の濃度(アレフ0)と 実数の濃度の間にも、中間の濃度があるのではないか? という議論があり、確定されていないのです 例えば、≪自然数と実数の間には 無限に異なる濃度が存在する≫ということが証明されたなら 新たな数学が成立する可能性もあるわけです しかし、自然数と実数の中間の濃度を表す集合は いまだ発見されていないそうです 「自然数と実数の中間の濃度はない」 だから「実数の濃度はアレフ1である」という考えを ≪連続体仮説≫と言います カントールの立場もこれにあたります もし、自然数と実数の中間の濃度がないとするならば アレフ2、アレフ3、アレフ4・・・・という概念は 以下とおり定義できるようです 例えば、F={1、2、3}という集合を 分解すると、どのような集合ができるでしょうか? {}(空の集合・全部入れない) {1}(2と3は入れない) {2}(1と3は入れない) {3}(1と2は入れない) {1、2}(3は入れない) {1、3}(2は入れない) {2、3}(1は入れない) {1、2、3}(全部入る) という8つの集合ができます F={1、2、3}の要素は、3つですが Fからは、8つの集合がつくれます こうしてつくれる集合を「べき集合」と言います Fの各要素(数字)について 「入れるべきか」 「入れないべきか」の2択を繰り返すので 2×2×2×・・・・という「2^要素数」で増えます (〇^n とは 〇 の n 乗 すなわち、〇 を n 回かけた数です) つまり F={1、2、3}からは、8個 F={1、2、3、4}からは、16個 F={1、2、3・・・・n}からは、2^n個 F={自然数}からは、2^自然数個 の「べき集合」がつくれることになります F={自然数(=無限個)}というのは 無限集合で、「アレフ0」と定義されています そこで アレフ0=自然数の濃度=2^自然数 アレフ1=実数の濃度=2^アレフ0 アレフ2=2^2^アレフ0 アレフ3=2^2^2^アレフ0 であると考えられています つまり、どれも無限個の要素をもつ集合ではありますが そこからつくれる「べき集合」の数によって アレフ0、アレフ1、アレフ2・・・・と ランクづけしたのが集合論の「無限」ということです アレフの定義を述べます 2つの集合 A と B があったとします A= {リンゴ、ミカン、イチゴ、カキ、ブドウ} B= {1、2、3、4、5} (1) 集合Aの各要素に対して、集合Bの要素が1つ対応する (2) Aの異なる要素に、Bの異なる要素が対応する (3) Bの要素に対して、必ずAのある要素が対応する この対応付けを全単射と言います 例えば、リンゴ→1 ミカン→3 イチゴ→2 カキ→4 ブドウ→5 という対応付けは全単射になります AからBへの全単射があるとは Aに入っている要素の数=Bに入っている要素の数 ということになります もし、(1)と(2)が成り立つ対応付けだけだと Aに入っている要素の数≦Bに入っている要素の数 もし、(1)と(3)が成り立つ対応付けだけだと Aに入っている要素の数≧Bに入っている要素の数 となり、全単射は存在しません つぎに B={1、2、3、4、5・・・・} とします 要するに、Bを自然数の集合とします Aを適当な集合とします もし、AからBへの全単射が存在するとき Aの濃度(要素数)を、アレフ0(アレフ・ノート)と言います 自然数は無限に存在するので もちろんアレフ0は、無限を表しています Aを(正の)実数の集合とすると AからBへの全単射は存在しません 正確に言うと、(1)と(2)が成り立つ対応付けがありません (1)と(3)が成り立つ対応付けはもちろんあります ということは Aに入っている要素の数 > Bに入っている要素の数 が成立します 要するに、同じ無限個の集合なのですが 自然数の集合よりも大きな集合があることになります こういう比較をして 無限個の集合に対してランク付けしたのが アレフ0、 1 、 2 ・・・・です フラクタル次元について ネットで調べてみると フラクタル次数とは、図形の複雑さを表す概念であり 図形が複雑であればあるほど数値が高いとか 対象の形態が複雑であるほど、D(次元)値は2に近づいていくとか いった記述がたくさん見られます しかし、正三角形や正方形といった ふつうの図形(複雑でもなんでもない図形)が、2次元であり シェルピンスキー三角が1.58次元 コッホ曲線が1.26次元と、訳の分かりません アルゴリズムと人工知能の教授にお尋ねすると ≪そもそもフラクタル次元って定義が一意じゃないですし 〇〇次元というやつがいろいろと定義されているはずです フラクタルを研究されている先生もいらっしゃったのですが 話を聞いても今一つピンときませんでした (^^;;; フラクタルにあまり価値を見出していないからなのか 話を聞いても頭に入ってこないんですよね 笑 ≫ ということでした 以上を踏まえた上で、私が調べたことをまとめると およそ以下のようなもののようです 最も有名なフラクタル次元は フェリックス・ハウスドルフ(1868~1942)という ドイツ数学者が提唱した「ハウスドルフ次元」です シェルピンスキー三角形の面積は0とされます 1回の操作ごとに3/4倍に減少し 無限回では →0 になるということです 操作を無限に繰り返すと、画像が真っ白になってしまうので 便宜上、適当なところで止めたものが描かれます 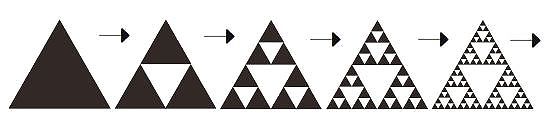 面積がないといっても、点とは違い 無限小の正三角形が、無限にあるとされます では、点(0次元)でもなく 線(1次元)でもなく、面(2次元)でもなさそうな 無限のチリの集まりのような図形は、果たして何なのか? といったような考えから、ハウスドルフ次元は出発しているようです コッホ曲線でいうと コッホ曲線の長さは無限大とされます そうなると線(1次元)のようではなさそうだし かといって平面(2次元)でもない 1次元の物体と考えるには大きすぎるし 2次元の物体であると考えるには薄すぎる そこで次元1と2の間の次元を考えてみた これがフラクタル次元(ハウスドルフ次元)の概念のようです 正方形の1辺の長さを1/2に縮小したら もとの正方形に戻すには 1辺の長さを1/2に縮小した正方形が4つ必要です 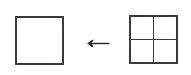 つまり、1辺の長さを1/2に縮小した正方形は もとの正方形の1/4の大きさ(面積)です 式にすると、(1/2)^D=1/4 D=2 です 正方形の1辺の長さを1/3に縮小したら もとの正方形に戻すには 1辺の長さを1/3に縮小した正方形が9つ必要です 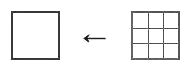 つまり、1辺の長さを1/3に縮小した正方形は もとの正方形の1/9の大きさ(面積)です 式にすると、(1/3)^D=1/9 D=2 です このD(ディメンション)が次元であり 正方形は、2次元ということです これが、フラクタル次元(相似次元)です 立方体の1辺の長さを1/2に縮小したら もとの立方体に戻すには 1辺の長さを1/2に縮小した正方体が8つ必要です 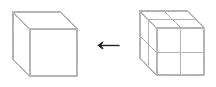 つまり、1辺の長さを1/2に縮小した立方体は もとの立方体の1/8の大きさ(体積)です 式にすると、(1/2)^D=1/8 D=3 です 立方体の1辺の長さを1/3に縮小したら もとの立方体に戻すには 1辺の長さを1/3に縮小した正方体が27個必要です 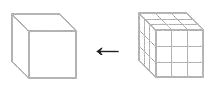 つまり、1辺の長さを1/3に縮小した立方体は もとの立方体の1/27の大きさ(体積)です 式にすると、(1/3)^D=1/27 D=3 です 立方体は、3次元ということです すなわち、相似次元(D)とは 1/r倍に縮小した図形を 何個(N)集めたら、もとの図形に戻せるのか? を考えたときの N=rのD乗 で表すことができます 正三角形で、考えると もとの正三角形の1辺の長さを1/2に縮小したら もとの正三角形に戻すには 1辺の長さを1/2に縮小した正三角形が4つ必要です 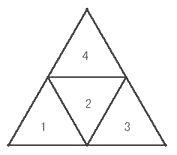 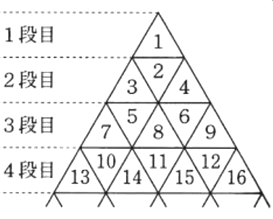 つまり、1辺の長さを1/2に縮小した正三角形は もとの正三角形の1/4の大きさです 式にすると、(1/2)^D=1/4 D=2 です 1辺の長さを1/3に縮小した正三角形は もとの正三角形の1/9の大きさです 式にすると、(1/3)^D=1/9 D=3 です フラクタル次元(相似次元)とは あくまで フラクタル図形(縮小した図形をあつめることで もとの図形にもどせる図形)についての単位であって 空間次元の2次元=平面 とは、似ているようで違います
さて、三角形の真ん中をくり抜く操作をしても 前段階の図形には戻りませんし 操作を繰り返しても もともとの三角形にも戻ることはありません 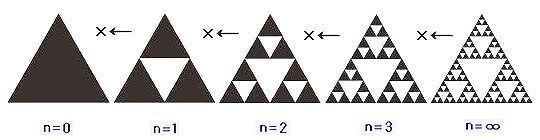 n=0 に、操作(真ん中をくり抜く)をすると もとの図形(n=0)には戻らず、n=1 になります n=1 に、操作(真ん中をくり抜く)をすると もとの図形(n=1)には戻らず、n=2 になります ところがシェルピンスキー三角形というのは 操作を無限回繰り返してできた図形なわけです そうなると、シェルピンスキー三角形にさらに 操作を1回繰り返しても、無限回操作したことには変わらず もとのシェルピンスキー三角に戻る という理屈が成り立ちます 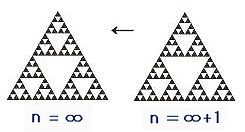 正三角形は 1辺を1/2に縮小した正三角形= 1/4の大きさ(面積)の正三角形 を 4つ集めると、もと図形に戻ります 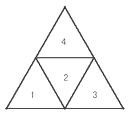 縮小コピー1/4が、構成単位 なので (1/2)^D=1/4 → D=2 2次元である となります これに対し、シェルピンスキー三角形は くり抜き操作=1辺の長さを1/2に縮小した 正三角形を3個つくる操作 をすると(をしても) もとの図形(シェルピンスキー三角形)に戻ります  縮小コピー1/3が、構成単位 なので (1/2)^D=1/3 → D=1.5849・・・・ シェルピンスキー三角形の フラクタル次元は、1.58次元 ということになります コッホ曲線の場合も同様です  n=0 に、操作(3等分したものを、4本集める)をすると もとの図形(n=0)には戻らず、n=1 になります n=1 に、操作(3等分したものを、4本集める)をすると もとの図形(n=1)には戻らず、n=2 になります ところが、n=∞(コッホ曲線)は 操作を無限回操作を繰り返してできた図形なわけです なのでさらに操作(3等分したものを、4本集める)を 繰り返しても、n=∞で、コッホ曲線(もとの図形)に戻るということです 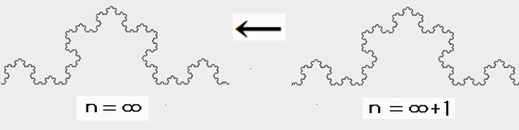 相似次元(D)とは 1/r倍に縮小した図形を、何個(N)集めたら、もとの図形に戻せるのか? を考えたときの N=rのD乗 で表すことができます コッホ曲線は 1/3に縮小した図形(線)を、4本集めても もとの図形(コッホ曲線)に戻ることから rが3、Nが4 となり 4=3^D が成り立ち D=1.2618・・・・ 1.26次元であるというわけです もう一度、コッホ曲線の次元についての考え方を 整理しておきましょう まず、無限回操作を繰り返したところに 何回同じ操作を繰り返しても無限回を超えない なので、もとの図形と同じである(もとの図形に戻る) というという考えを基盤としています そこから 正方形は、1/2の図形を4個あつめれば あるいは、1/3の図形を9個あつめれば もとの正方形に戻る 同様に、無限回操作を繰り返したコッホ曲線は 1/3の図形を4つあつめれば もとの図形(コッホ曲線)に戻る とし、同じ式に当てはめて 次元を割り出しているのです 但し、無限回操作を繰り返したコッホ曲線に 別の操作を行うとコッホ曲線にはなりません。別の図形になります すなわち、同じ操作(1/3の図形を4個あつめる)をすることで コッホ曲線になるわけです つまり、正方形は、1/2の図形を4個あつめれば もとの図形に戻せる図形になっているのと同様に コッホ曲線は、1/3の図形を4個あつめれば もとの図形(コッホ曲線)に戻せる図形になっているの ということです 1/r倍に縮小した図形を、何個(N)集めたら、もとの図形に戻せるのか? でいうと、rが3、Nが4の図形になっている ということです
無限回操作を繰り返すと、空間充填曲線となり ヒルベルト曲線(空間充填曲線)のフラクタル次元は2次元です 点のハウスドルフ次元は0、線分のハウスドルフ次元は 1 正方形のハウスドルフ次元は2 立方体のハウスドルフ次元は3とされるので 空間充填曲線は、正方形と同じという理屈です なお、空間充填曲線は イタリアの数学者 ジュゼッペ・ペアノ(1858~1932)による 「ぺアノ曲線」の発見が最初です 無限回操作で空間充填曲線になるとされます  ヒルベルト曲線はペアノ曲線の変種で、より複雑化したもののようです Wikipediaに、フラクタル次元について ≪フラクタルがどれだけ完全に 空間を満たしているように見えるかを示す統計的な量≫とあり フラクタル次元というのは 形状の複雑さというよりも 「空間を満たす度合い」をいうようです ホログラフィック理論のデタラメを暴く フラクタルの理論について ① (ひとつ戻る) |
|